The-5-Platonic-Solids-or-Regular-Solids

The 5 Platonic Solids or Regular Solids

by

Geometry – the study of shapes, sizes, positions, angles, and dimensions of things – has fascinated people since ancient times. From history books, we see shapes and their application by among others the Romans, Egyptians, and Neolithic communities. Of these shapes, one special group has been given more attention, The Five Regular Solids (Platonic Solids).

Man’s interest in Geometric shapes led to the invention of solids such as the Icosahedrons and Dodecahedron. Evidence of these shapes includes the carved stone balls in Scotland and the twenty-sided die (icosahedron) in Egypt.

Around 360 BC, Plato, an ancient Greek Philosopher, first described the icosahedron in his essay Timaeus. According to his student Aristotle, Plato may have learned about these shapes from Pythagoras. But because he was the first to assign them to the universe, these regular solids were named after him.

According to Plato, the five regular solids exist in the universe and represent the five Nature elements i.e. Fire, Earth, Air, Water, and the Heavens. This could be true if you consider that it’s from these same solids that we get the Flower of Life (Sacred Geometry) represented by Metatron’s Cube.

Twenty-sided-die

Geometry: Shapes

To understand these solids, let’s first learn a few basics of geometry:

Plane Geometry

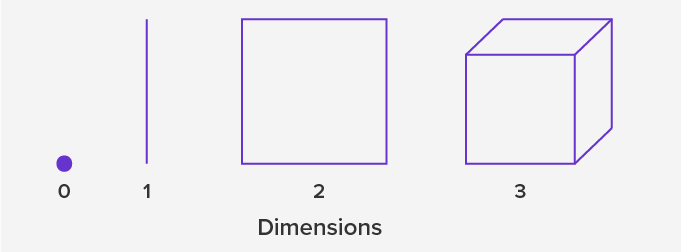
  1. A Point in geometry is a position or location. It has no dimensions, no size. (Represented by a dot).
  2. A Line is one-dimensional (1D). It is straight and extends in both directions infinitely.
  3. A Plane is two-dimensional (2D). It is a flat surface with no thickness.
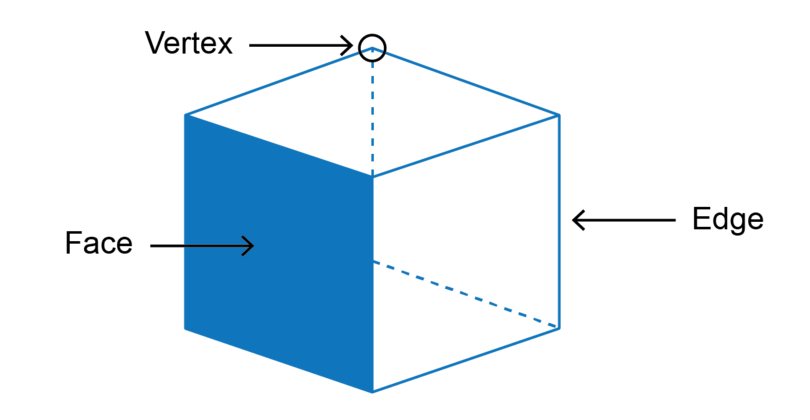
  4. A Solid is three-dimensional (3D). It has a width, depth, and height. Besides surface area and volume, solids have other properties such as vertices, faces, and edges.

point, line and Plane

Solid Geometry

  1. An edge (E) is a line segment between faces.
  2. A vertex (V) is a corner (Point where edges meet).
  3. A face (F) is a single flat surface.
  4. A Polyhedron (Polyhedra) is solid with many (poly) flat faces (hedron). Examples of polyhedra include platonic solids, prisms, and pyramids.
  5. A solid is Non-Polyhedra if any of the surfaces are not flat like in the case of a Cylinder, Sphere, or Cone.

Solid Geometry

Euler’s Formula F + V = E + 2

Properties of Platonic Solids

  1. Faces are equal and Identical, regular polyhedrons.
  2. Faces only intersect at their edges.
  3. The same number of faces meet at each vertex.

Why do we have only five regular solids?

  1. All solids are three-dimensional 3D and so, at least 3 faces must meet at each vertex.
  2. To avoid overlapping, internal angles at any vertex must add up to less than 360°.
  • A regular triangle has internal angles of 60°.
  • A square has internal angles of 90°.
  • A regular pentagon has internal angles of 108°.

The-five-regular-polyhedra

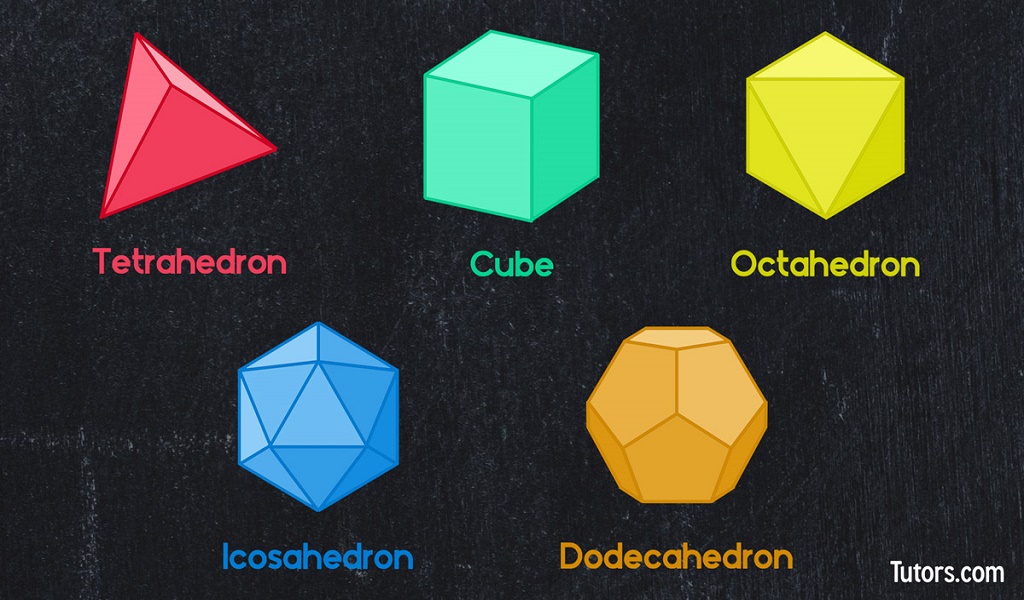
The 5 regular solids or platonic solids

With the basics out of the way, let us look at the 5 regular solids.

1. Tetrahedron

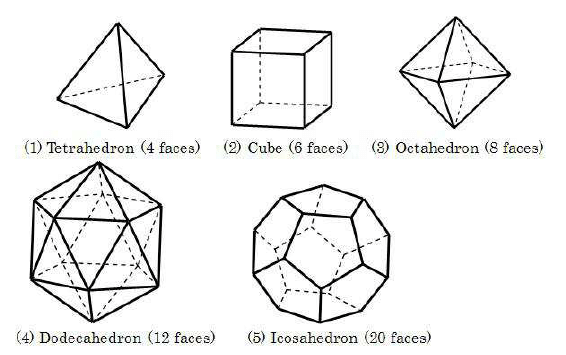
The Tet is the simplest of the shapes. It has four equilateral triangular faces, joined along six edges to form four vertices (4 Faces, 4 Vertices, 6 Edges). You can think of it as a pyramid. Plato associated the tet with Fire because of its pointed vertices.

2. Cube

Also called the Hexahedron, a Cube has 6 square faces, 8 Vertices, and 12 Edges. It is the shape of Earth.

3. Octahedron

The Oct is a polyhedron with 4 triangles meeting at each vertex. It has 8 faces, 6 Vertices, and 12 Edges. According to Plato and Pythagoras, the Oct symbolizes Air.

4. Dodecahedron

With 3 pentagons meeting at each vertex, the Dodeca has 12 Faces, 20 Vertices, and 30 Edges. It is the most complex of the solids to construct. According to the mathematicians, it represents the Heavens.

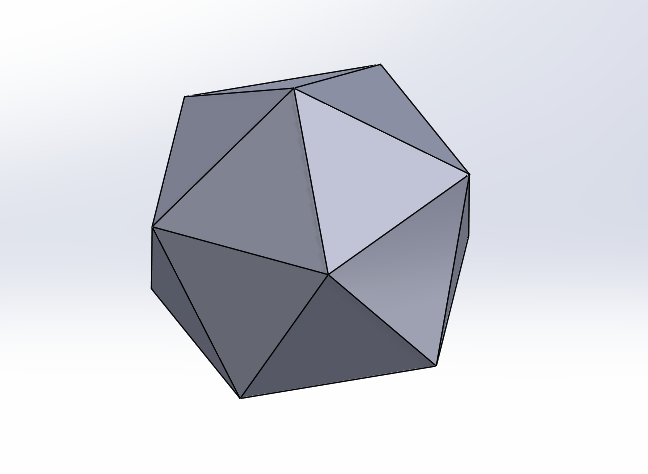
5. Icosahedron

The Icosa has Five triangles meeting at each vertex. With 20 Faces, 12 Vertices, and 30 Edges this is one of the most useful polyhedra. The Geodesic Dome and Traditional Soccer Ball are some of the things derived from the Icosa. It represents Water.

The Icosahedron
The Icosahedron [Credit: Google Sites]

DIY Time

  1. Use the Euler’s Formula to determine the number of edges in each solid.
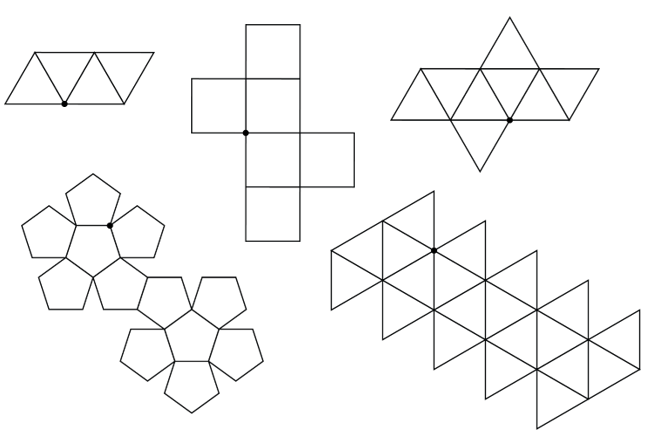
  2. Using Drinking Straws, Construct the 5 Regular Solids. (See nets below)
  3. Share your final models with me via info@leogichuki.com

Credits

  1. Carved stone balls from Scotland [Credit: Ashmolean Museum]
  2. Five Elements [Credit: https://hellenicfaith.com]
  3. Twenty-sided die (icosahedron) [Credit: The Metropolitan Museum of Art]
  4. 5 Platonic solid [Credit: tutors.com]
  5. Math is Fun https://www.mathsisfun.com/index.htm
  6. Solid Geometry https://ng.siyavula.com/

FUN FACT: The traditional Soccer ball is a Truncated Icosahedron!

Leave a Comment